二维转角莫尔超晶格中的拓扑量子态研究：attocube专题应用白皮书

发布日期：2025-07-01

摘要

范德瓦耳斯（vdW）莫尔双层材料是研究陈绝缘体物性的理想平台。本白皮书系统阐述attocube低温测量系统在二维莫尔超晶格拓扑量子态研究中的关键技术突破。通过整合标志性研究成果，重点展示范德瓦耳斯双层体系中的整数与分数量子莫尔陈绝缘体（MCIs）：

• 对整数型MCI材料MoTe₂/WSe₂的扫描磁力测量表明^[1]，其磁化强度可通过极弱电流翻转，为高能效磁存储器提供新路径；

• 同种异质结构的磁光研究^[2]揭示了该材料量子反常霍尔态具有谷相干特性；

• 扫描单电子晶体管（SET）研究^[3]构建了魔角扭曲双层石墨烯（MATBG）的高场相图，该材料此前被确认为高场整数MCI^[4]；

• 扫描磁力测量发现^[5]，填充因子变化导致的贝里曲率局域调制会形成不同陈数的MCIs镶嵌结构；

• 在低磁场（B<12T）条件下，MATBG仍可实现分数量子陈绝缘态（FCIS）^[6]；

• 基于Trion探测的磁光技术^[7]，在扭曲双层MoTe₂中观测到零磁场（B=0）下稳定存在的FCIS。

背景介绍

魔角扭曲双层石墨烯（MATBG）中超导相与可调控类莫特绝缘相的发现^[8]，确立了莫尔双层体系是实现强关联电子态与拓扑量子现象的理想平台。二维超晶格构建主要有两种方式：一是在扭曲双层石墨烯或扭曲双层MoTe₂中，将两片相同材料层旋转错位堆叠；其二是堆叠晶格常数存在微小差异的双层材料（如MoTe₂/WSe₂）。由此形成的莫尔超晶格具有高度平直的能带结构，且通过巨大的单粒子能隙与其他能带分离，这一特性为观测奇异准粒子激发态（如分数量子霍尔效应中的任意子）提供了关键条件。

在开创性研究^[9]中，Duncan Haldane颠覆了"实现类量子霍尔态必须依赖磁场B"的传统范式，该态需具备平直能带色散及强电子相互作用。他证明通过引入晶格位点间的次近邻跃迁（NNNH，作用于动量空间K与K'点）可实现时间反演对称性破缺。这正是莫尔双层体系中的关键机制——动量空间的微布里渊区（MBZ）显著增强了NNNH效应。MBZ在实空间的倒易结构即莫尔超晶格，其周期通常为原子间距的10-100倍。因此当霍尔电阻量子化且纵向电阻消失时（即便在零磁场B=0条件下），莫尔双层将呈现奇异拓扑现象，此效应称为量子反常霍尔（QAH）效应。展现QAH效应的材料作为拓扑绝缘体的子类，被统称为陈绝缘体（CI）。相较于磁性掺杂拓扑绝缘体，这类材料在零磁场和相对较高温度（~0.1-10K）下展现的拓扑特性，使其成为研究拓扑性与强关联电子现象（如超导性和莫特物理特性）相互作用的典范体系。

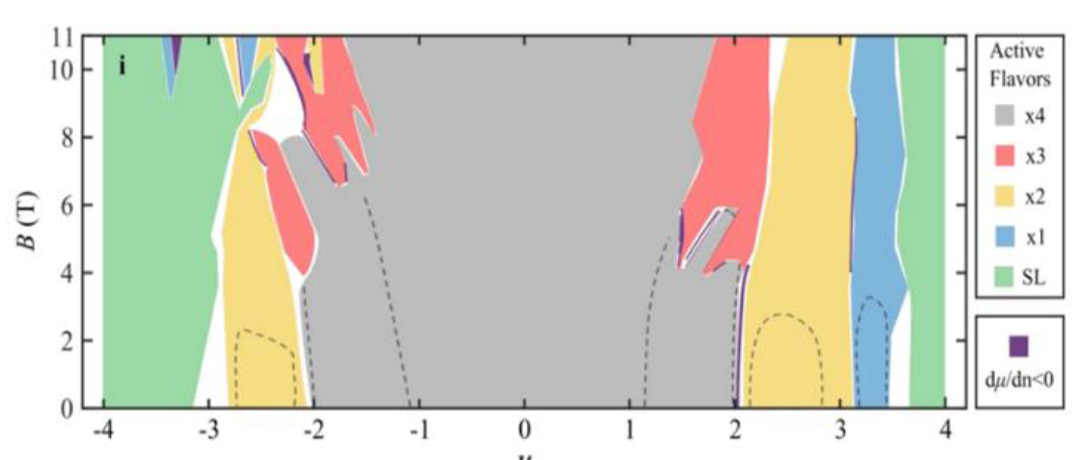
Fig 1: Phases of Chern insulator in MATBG, corresponding to 4 possible combinations of spin and valley flavours. Green area is where all spin and valley values are simultaneously active. Filling factor ν is number of electrons per moiré superlattice site. Dashed lines engulf regions of non-anomalous quantum Hall effect ^[3].

此类多功能体系亟需能精确探测物相及其关联的实验手段，而 attocube 的核心价值正在于此 —— 提供可在极端条件下实现高精度复杂测量的系统解决方案。下文将重点展示客户实验室利用attocube设备取得的突破性成果，这些发现深刻揭示了莫尔双层中陈绝缘体物相的本质特性。研究聚焦于扫描探针与磁光测量两大精密技术领域，此类测量要求：在低温变温与强磁场极端环境中，必须具备亚微米级定位精度、超低振动噪声及接近零漂移的稳定性，而这正是attocube技术的核心优势所在。

技术成果：

1. 莫尔陈磁体中的电流驱动磁化翻转

莫尔陈磁体已被打造为低电流磁开关的工程平台，在磁存储器领域具有重要应用前景。在莫尔异质结构中，特定有理数电子/空穴填充下，时间反演对称性破缺与强库仑排斥协同作用可诱导陈绝缘态。美国加州大学圣塔芭芭拉分校安德烈·杨（Andrea Young）课题组联合康奈尔大学Kin Fai Mak与Jie Shan团队^[1]，致力于解析扭曲单层-双层石墨烯体系[10]中低电流磁化翻转的微观机制。

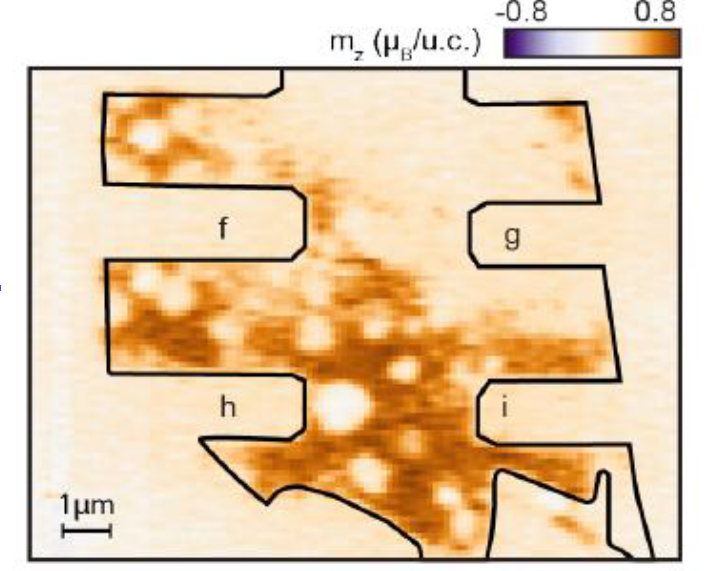
Fig 2. 2D map of magnetization at QAH phase measured with a nanoSQUID-on-tip sensor using attocube nanopositioners ANPx101, ANPz101 and ANSxy100 ^[1]

本研究探讨了一种三层莫尔超晶格体系——该结构由双层MoTe₂与单层WSe₂以60°相对晶体轴排列堆叠而成。当体系在1.6 K温度下施加垂直强电场且空穴填充因子维持在ν = -1时，可进入量子反常霍尔态（QAH态）。研究人员通过输运测量和纳米超导量子干涉仪探头（nSOT）显微技术，对零磁场条件下观测到的陈磁体态展开研究：该态具有近乎量子化的反常霍尔效应，纵向电阻趋近于零，并展现出滞后电流行为特征。

采用石英管尖端铟基纳米SQUID（结合压电音叉驱动，磁场灵敏度15 nT/Hz1/2对实空间磁序成像，揭示了电流翻转的微观机制。通过3 kHz全局背栅电压调制，nSOT探针成功捕获磁序衍生的边缘磁场调制δB。当施加ISD = 670 nA电流时，磁化强度局域变化成像显示磁畴反转与驱动电流存在精确关联。基于小交流电流的局域磁响应测量，观察到电流驱动的磁畴翻转机制源于本征自旋霍尔效应：该效应扰动磁序并向平衡磁矩施加力矩，最终导致陈磁体局域磁化反转。该体系磁化翻转仅需j < 103 Acm^-2的创纪录低电流密度，较现有自旋轨道矩系统降低三个数量级。Attocube公司的低温纳米位移台ANPx101, ANPz101 and ANSxy100 在此项工作中发挥了重要作用。

2. 自旋极化与能谷相干陈态的自发形成

魔角扭曲双层石墨烯（MATBG）中的量子反常霍尔效应（QAH）源于相互作用驱动的能谷对称性破缺，其基态呈现能谷极化特性。然而，在堆叠过渡金属硫族化物（TMD）异质双层结构中，反演对称性破缺与强自旋轨道耦合可在单层内诱导独立的陈能带。当体系进入QAH态时，层间耦合将导致能谷陈能带维持极化或转变为相干态——这成为关键科学问题。美国康奈尔大学Jie Shan和Kin Fai Mak课题组与斯坦福大学托尼·海因茨（Tony Heinz）课题组合作，通过层分辨与螺旋度分辨光谱技术结合输运测量，在AB堆叠MoTe2/WSe₂莫尔超晶格双层结构中对该问题展开研究^[2]。光学选择定则决定了吸引型谷极化子与探测圆偏振光螺旋度的耦合方式，从而调控堆叠层间谷极化或谷相干性的产生。研究首先将TMD双层体系制备成每个晶格位点填充一个空穴(v = -1)的莫特绝缘态，随后施加垂直电场诱导拓扑相变，使系统进入陈绝缘体(CI)态。在CI态下，通过层分辨与螺旋度分辨的光反射对比度(RC)测量，在-8T至8T磁场范围内进行能量扫描。零磁场条件下，吸引型谷极化子在两层中均主要响应σ⁻螺旋度的激发光，该现象证实了体系存在谷相干性及自旋极化。当施加非零磁场时，两层中的自旋与磁矩排列均表现出对激发光螺旋度相同的响应规律。

通过磁圆二色谱（MCD）随磁场B变化的深入研究，发现当B=0时，WSe₂层和MoTe₂层分别达到45%和60%的自旋极化度即足以实现量子化霍尔电阻。此外，变温MCD实验揭示了自旋织构特征及热涨落效应：自旋磁化率的温度依赖性严格遵循居里-外斯定律，这一结果强有力地支持了陈绝缘体（CI）态双层体系中存在倾斜自旋织构（具有非零面内分量）的突破性发现。该发现为理解AB堆垛型TMD莫尔双层的CI相磁基态开辟了新途径。

实验采用attoDRY2100共聚焦系统构建低温（1.6 K）低振动环境。

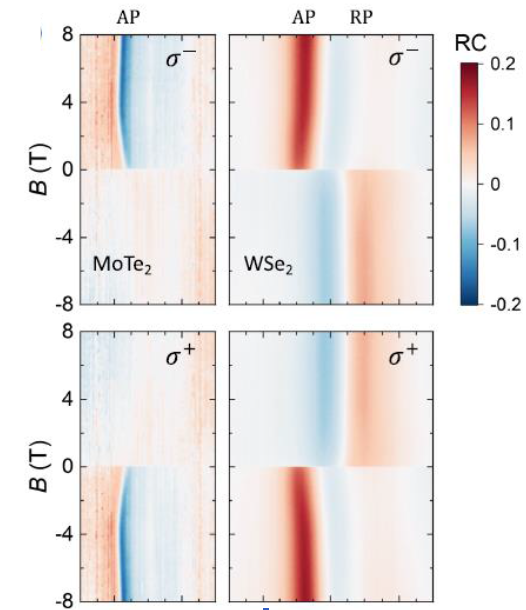Fig 3. Magnetic field dependence of reflectance contrast spectrum w.r.t helicity(σ+ or σ-)   of MoTe₂/WSe₂ bilayer measured in attoDRY2100 ^[2].

3. 在MATBG体系中强关联拓扑相的识别

在强垂直磁场作用下，莫尔双层体系中占据分形霍夫斯塔特能子带的竞争拓扑态随电子占据数变化，已成为凝聚态物理领域极具吸引力的前沿课题。当研究魔角石墨烯双层（MATBG）中自旋/谷自由度的占据数演化时，其拓扑相变过程呈现出更为丰富的物理图景。斯坦福大学本杰明·费尔德曼、沈志勋与史蒂文·基弗森联合团队通过扫描单电子隧穿显微技术，在1.7K极低温下测量局域电子压缩率倒数dμ/dn，首次完整绘制出这些竞争拓扑态间的霍夫斯塔特能谱及热力学相变图谱^[3]。

通过施加垂直磁场（0-11 T）并调节莫尔超晶格填充因子（v = −4 → 4），获得了Wannier相图。该相图显示了一系列具有能隙的不可压缩态，其范围从电荷中性点（CNP）起源的朗道能级（LL）对应的量子霍尔态，一直延伸到高磁场下从未报道过的新型关联陈绝缘体（CI）态。观测到不同的陈绝缘体态在万尼尔相图的特定区域相交，这表明了单粒子机制和相互作用驱动的对称性破缺之间存在竞争。通过积分局域压缩率获得的、表征热力学多体能级的化学势 μ(n, B)（费米能）被用来在实验上确定相互作用的霍夫施塔特（Hofstadter）能谱；通过观察态密度中类范霍夫奇点（vHs-like）的特征，可以清晰地区分出其中的相变。

本工作的核心成果是构建了魔角石墨烯（MATBG）的相互作用Hofstadter相图。作者提出了一种基于flavour的对称性破缺机制，该机制与实验数据高度吻合。这种对魔角石墨烯中不同陈绝缘体（CI）相的统一框架，对于理解由flavour polarization所主导、并随载流子密度（density）和外加磁场（applied magnetic field）变化的相变内在机制具有极其重要的价值。attocube 低温纳米位移台ANPx101 在此工作中起到了重要的作用。

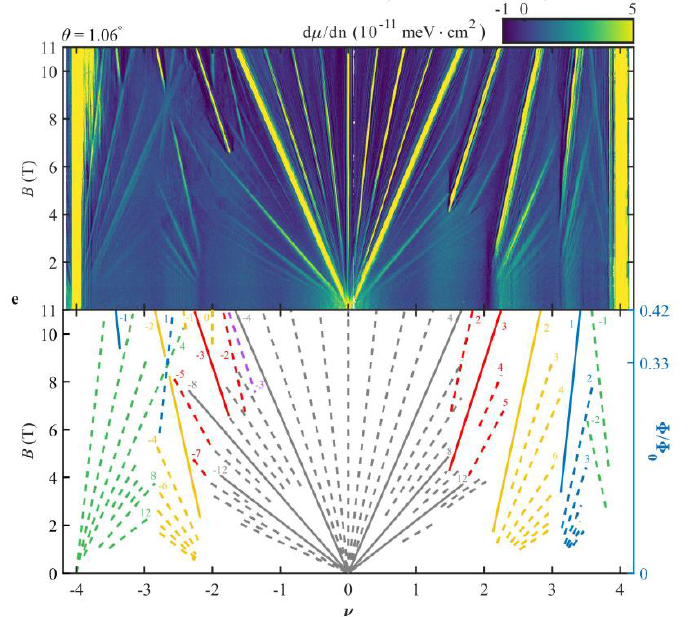
Fig 4. Fan diagram of inverse electronic compressibility (dμ/dn) vs magnetic field B and lattice filling measured with a scanning SET sensor using attocube nanopositioners ANPx101 ^[3]. Wannier diagram is shown below the measurement data.

4. 在MATBG体系中陈数局域变化的显微观测

陈绝缘体（CIs）的特征在于陈数（Chern number）——这是一种拓扑不变量，源于在时间反演对称性破缺条件下，跨越有能隙能带的扩展贝里曲率（Berry curvature）。然而，理论预言表明，在摩尔双层材料中，由于空间变化的衬底势，预计会发生局部陈数的变化。魏茨曼科学研究所（以色列）的Eli Zeldov研究组和ICFO（西班牙）的Dmitri Efetov研究组，通过使用一个故意未与hBN衬底对齐的魔角双层石墨烯（MATBG）样品，测绘了跨越一系列金属态和有能隙态（作为摩尔填充因子υ的函数）的平衡态局域轨道磁性，从而验证了这一假说 ^[5]。

输运实验显示在υ = 1附近横向电阻出现了显著且非平凡的滞回现象，表明存在轨道磁性和反常霍尔效应（AHE）。二维磁成像通过使用铟制尖端超导量子干涉仪（SOT） 实现，该SOT在样品表面上方约160 nm高度进行扫描，并在垂直于样品表面的50 mT外磁场存在下工作。成像是通过测量由调制背栅电压引起的局域磁信号变化获得的。数据揭示了整个样品中存在许多具有不同陈数的斑块（patches）。

在υ = 0.966时，局域微分磁化数据揭示了复杂的图案，该图案由对外部磁场呈现正（类顺磁性） 和 负（类抗磁性） 响应的孤立斑块组成。在υ = 1附近的一系列填充因子范围内，这种图案的出现和发展清晰可见。观察到的由两种类型斑块构成的镶嵌图案（作者称之为“陈数马赛克”（Chern mosaic））被认为可能由以下两种机制形成：

• 在υ = 1附近，由于hBN衬底势与石墨烯摩尔晶格incommensurate导致的空间变化势，引起自发的子晶格对称性破缺；

• 石墨烯层间以及hBN层与相邻石墨烯层之间的扭转角，可以形成nearly commensurate的摩尔晶格，进而产生周期性的子晶格极化。这一点再结合应变、结构弛豫和结构无序，可能导致非均匀的局域陈能带，从而产生陈数马赛克图案。

这一结果表明，除非特意制备与hBN衬底精确对齐的MATBG样品，否则此类拓扑无序在MATBG器件中普遍存在。此研究采用attocube扫描探针显微镜控制器ASC500，配合纳米位移台ANPx101、ANPz102与ANSxy100获取磁成像数据。

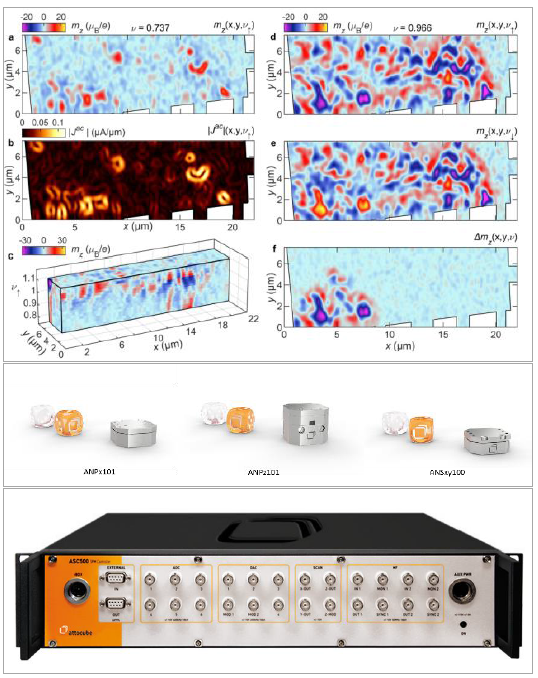
Fig 5. Imaging local magnetization and reconstructed equilibrium current density across MATBG sample with nanoSQUID sensor using attocube nanopositioners ANPx101, ANPz102 and ANSxy100. Scan control and data acquisition has been performed using attocube scanning probe microscopy controller ASC500 ^[5].

5.在 MATBG系统中分数量子陈绝缘体态的观测

由强关联二维电子系统（例如，高磁场下的分数量子霍尔效应（FQHE））承载的任意子，因其奇异的交换统计特性，被认为在执行容错拓扑量子计算方面极具应用潜力。在二维摩尔（moiré）系统中，分数陈能带（fractional Chern bands）被认为能够在极低磁场下承载任意子，理论上甚至在零磁场（B = 0）下也能实现。

本工作中，作者报道了在低至 5 T 的磁场下，在魔角石墨烯（MATBG）中观测到分数陈绝缘体（FCI）态。来自哈佛大学（美国）的 Amir Yacoby 研究组和麻省理工学院（MIT，美国）的 Pablo Jarillo-Herrero 研究组，利用扫描单电子晶体管（SET）装置，对扭转角约为 1.06° 的 MATBG 样品进行了逆压缩率测量（测量平衡态下的 dμ/dn）^[6]。

所获得的Wannier相图（以摩尔填充数 ν 和外加垂直磁场 B 为变量绘制的能隙态分布）显示了一系列线性色散（linearly dispersing）的不可压缩态（incompressible states）。这些态可根据满足Diophantine equation） υ = tφ / φs+s 的元组 (t, s) 进行分类。在包括整数量子霍尔态、电荷密度波（CDW）态和对称性破缺陈绝缘体态在内的五类不同的不可压缩态中，最引人注目的是仅取分数 t 值和 s 值的分数陈绝缘体（FCI）态。通过扫描填充因子从 -4 到 4 以及磁场最高至 12 T 的范围，总共观测到了八个分数陈绝缘体（FCI）态。

特别引人注目的是两个可一路低至 5 T 磁场下观测到的 FCI 态：(2/3, 10/3) 和 (1/3, 11/3)。这两个态可以看作是 1/3 和 2/3 分数量子霍尔效应（FQHE）态在晶格系统中的类比物（analogue），它们在填充因子范围 3 < υ < 4 内被观测到。通过将（逆压缩率测量得到的）对电子密度积分并乘以预期的准粒子电荷 e/3，得到这两个态的能隙均达到了 50 ± 20 μeV，这与理论预测大致相符。

为了理解电荷密度波（CDW）态与 FCI 态之间的竞争，进一步的研究揭示出：源于 AA 堆叠区域和 AB 堆叠区域之间层间隧穿（interlayer tunnelling）的贝里曲率（Berry curvature）非均匀性存在一个上限，这个上限决定了这两种竞争态之间的相边界。这解释了为何在该 MATBG 样品中需要施加磁场才能观测到 FCI 态。

另外六个 FCI 态主要在空穴掺杂区域（−3 ＜ υ ＞ 1）以及更高的磁场下被观测到。在这六个态中，识别出了一些没有对应的 FQHE 类似态的 FCI 态，特别是那些参数 t 和 s 的分母为互质数（co-prime） 的态。这一发现为专门在 MATBG 系统中研究陈绝缘体（Chern insulator）的奇异物相（exotic phases）开辟了新的途径。Attocube 低温纳米位移台在此实验中发挥了重要作用。

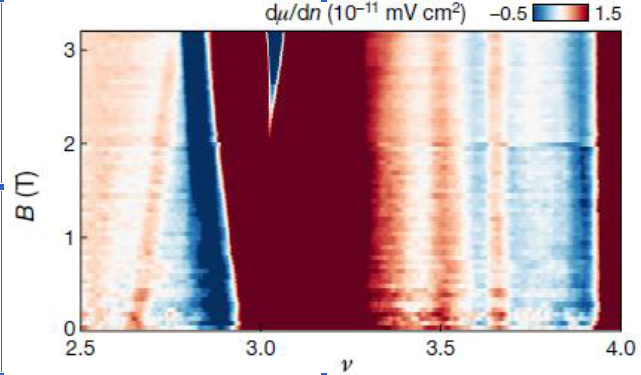
Fig 6. Mapping charge density waves by inverse electronic compressibility with scanning SET sensor using attocube nanopositioners ANPx101 and ANPz101 ^[6].

6.  在B =0中分数量子陈态的观测

这项研究首次展示了一种实验特征，证明了在零磁场（B = 0）下长期追寻的分数陈绝缘体（FCI）态在莫尔双层材料中的存在。基于先前在菱面体堆叠的扭转二碲化钼（MoTe₂）双层结构中观察到的具有时间反演对称性破缺的电可调铁磁态 [11]，作者们利用光学探测方法研究了该系统在空穴掺杂区的性质。

由美国华盛顿大学徐晓东（Xiaodong Xu）领导的研究小组采用反射磁圆二向色性（RMCD）技术，研究了围绕晶格填充数 ν = -1 和 -2/3 的铁磁态相空间，这些态是外加垂直电场和磁场的函数 ^[7]。他们确认了一个普遍存在的磁性相，其范围从 υ = -1.2 延伸到 υ = -0.4。通过测量 RMCD 磁滞回线，进一步支持了铁磁性的观测。

为了确定和表征能隙态（即绝缘态），作者们采用了一种探测三子（trion）光致发光（PL）的技术 ^[12]。光谱积分PL强度随磁场和掺杂（υ）变化的图像清晰地显示出在 υ = -1 和 υ = -2/3 处具有线性色散关系，其斜率分别为 -1 和 -2/3。该图像还显示了在 υ = -3/5 和低磁场值下存在一个较弱的色散特征，其陈数 C = -3/5。最令人兴奋的观察是，陈数为 C = -2/3 的态一直持续到 B = 0，这为实现零磁场下的阿贝尔任意子（Abelian anyons）并将其耦合到超导电路铺平了道路。此外，通过施加垂直电场，作者们观察到了 C = -1 和 C = -2/3 的陈绝缘体（CIs）发生的拓扑相变。此实验采用attoDRY2100低温恒温器构建低温（1.6 K）低振动测量环境，并利用attoCFM I系统进行光学测量。

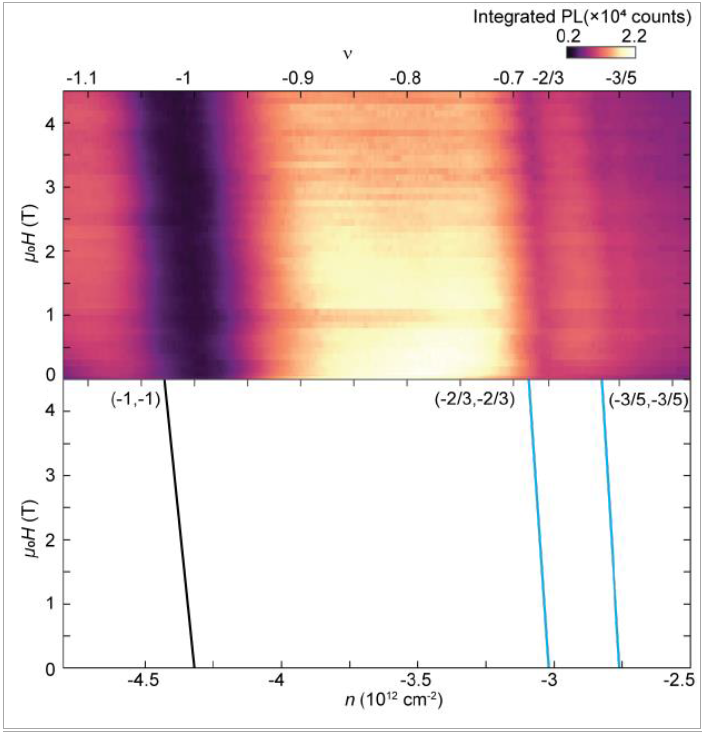Fig 7. Optical Landau fan diagram with integer and fractional QAH states in twisted MoTe₂ bilayer, revealed by utilizing an attoCFM I and an attoDRY2100 ^[7].

总结

量子霍尔效应（Quantum Hall effect）是量子物理学中拓扑现象研究的典范，因此一直备受关注。然而，由于其所需的极端环境条件（如强磁场、超低温和超高真空），相关的实验研究一直充满挑战。随着二维材料中陈绝缘体（Chern insulators）的实现，使得在中等强度磁场下、无需超低温和超高真空环境即可开展量子霍尔效应的基础研究成为可能。

attocube 的低温设备恰好能满足此类适中的环境要求，并已为陈绝缘体领域带来了显著的科研成果，本白皮书即为佐证。attocube 系统的低温纳米定位与纳米旋转装置适用于陈绝缘体的纳米尺度研究，因为它们能提供了超卓的稳定性，并配备超低振动低温恒温器。这些低温扫描装置包括共聚焦显微镜以及各种扫描探针显微镜，例如磁力显微镜（MFM）、超导量子干涉仪显微镜（SQUID microscope）、氮空位显微镜（NV microscope）、单电子晶体管显微镜（SET microscope）、微波阻抗显微镜（MIM）和量子扭转显微镜（QTM）。

参考文献

[1] L. Tschirhart, E. Redekop, L. Li, T. Li, s. Jiang, T. Arp, O.Sheekey,T. Taniguchi, K. Watanabe, M.E. Huber, K.F. Mak,I. Shan and A.F. Young, Nature Physics 19,807(2023)

[2]Z. Tao, B. Shen, s. Jiang, T. Li, L. Li, L. Ma, w. Zhao, 」. Hu, K.Pistunova, K. Watanabe, T. Taniguchi, T.F. Heinz, K.F. MakandJ.Shan,Physical ReviewX14,011004(2024)

[3]J. Yu, B.A. Foutty,Z. Han, M.E. Barber, Y. Schattner, K.B]Watanabe,T.Taniguchi, P, Phillips,Z.-X.Shen,S.A. Kivelsonand B.E.Feldman, Nature Physics 18,825(2022)

[4]K.P.Nuckolls,M.Oh,D.Wong,B. Lian, K. Watanabe, T.Taniguchi, B.A. Bernevig and A. Yazdani, Nature 588, 610(2020)

[5]S.Grover, M. Bocarsly,A. Uri, P.Stepanov, G. Di Battista, l.Roy,」. Xiao,A.Y. Meltzer, Y. Myasoedov, K. Pareek, K.Watanabe,T. Taniguchi, B. Yan, A. Stern, E. Berg, D.K.Efetov and E.Zeldov, Nature Physics 18,885 (2022)

[6] . Xie,A.T. Pierce,」.M. Park, D.E. Parker, E. Khalaf, P. Ledwith,Y. Cao,s.H. Lee,s. Chen, P.R. Forrester, K.Watanabe,T. Taniguchi, A. Vishwanath, P. Jarillo-Herreroand A. Yacoby,Nature 600,439(2021)

[7] J. Cai, E.Anderson, C. Wang, X.Zhang, X. Liu, w. Holtzmann,Y. Zhang, F. Fan,T.Taniguchi, K. Watanabe, Y. Ran, T. Cao,L. Fu, D. Xiao, w. Yao and X. Xu, Nature 622,63 (2023)

[8] Y. Cao,V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E.Kaxiras and P.Jarillo-Herrero, Nature 556,43(2018)

[9] F.D.M.Haldane,Physical Review Letters 61,2015(1988)

[10]H.Polshyn,」.Zhu,M.A. Kumar, Y. Zhang,F. Yang,C.LTschirhart, M. Serlin, K. Watanabe, T. Taniguchi, A.H.MacDonald and A.F.Young, Nature 588,66(2020)

[11] E. Anderson, F.-R. Fan, 」. Cai, w. Holtzmann, T. TaniguchiK.Watanabe, D. Xiao, W. Yao and X.Xu, Science 381,325(2023)

[12] A. Popert Y. Shimazaki, M. Kroner, K. Watanabe, TTaniguchi, A.lmamoglu andT.Smolenski, Nano Letters 227363(2022)